International Journal of Electrical and Computer Systems (IJECS)

ISSN: 1929-2716

1. Introduction

The propagation of electromagnetic wave through a medium is controlled by the medium's electric permittivity and magnetic permeability. Although the permittivity and permeability are positive in natural materials at microwave frequencies, metamaterials are artificial materials whose electromagnetic properties can be engineered to be effectively negative. Artificial Magnetic Materials (AMMs) are a type of metamaterials which exhibit magnetic material properties not found in nature as previously shown (Pradeep et al., 2011). In fact, the strong interest in such material lies in it being an enabling technology in several key applications. These emergent applications are using metamaterial blocks as a substrate for enhancing low-profile antenna performance (Buell et al., 2006), as a probe for near-field sensing (Boybay et al., 2008), for shielding applications (Lovat et al., 2007) and microwave absorbers (Bilotti et al., 2008) and many other applications.

An ensemble of metallic broken-loop resonators aligned in parallel planes normal to their surface and in a host dielectric is considered as an AMM. The magnetic dipoles generated in rings due to the magnetic field radiation are responsible for effective magnetic response of the medium. Artificial Magnetic Material (AMM) consist of metallic broken-loop inclusion which of incident magnetic field. Circular split-ring resonators (SRRs) and Swiss Roll resonators (SRRs) are common form of AMM's inclusions, originally purposed by Pendry et al. (1999). Split-ring resonators (SRRs) consists of two rings which separated by a gap and having splits on the opposite sides. The open metallic loop behaves as an LC resonator as shown by Kabiri et al. (2010). The area of the inclusion corresponds to its inductive behavior and its perimeter corresponds to the capacitive response. The area and perimeter in SRRs are dependent resulting in the dependency of the circuit-based equivalent capacitance and inductance of SRRs. Due to this restricted geometrical characteristic of SRRs, they are not capable of providing a full range of magnetic response; hence, limited to a random uncontrollable magnetic response. To generate a specific magnetic response of an AMM, the capacitance and inductance of inclusions needs to be tuned independently as confirmed by Khan and Mughal (2009).

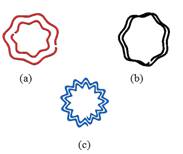
Kabiri et al. (2011) proposed a generic inclusion's geometry called n^th order rose curve resonator (n-RCR) which provides a full control on design of a desired magnetic response achievable by AMMs. RCRs are a generalized form of SRRs. The zeroth order RCR geometry has a circular shape identical to SRR. However, higher order RCRs have a circular base with a deformed sinusoidal perimeter providing extension to the perimeter of the inclusion while keeping the area constant. By tuning the order and amplitude of the deformation one can generate any desired magnetic properties achievable by AMMs. In addition, different topologies of inclusions have been proposed in the literature as proposed by Baena et al. (2004). RCRs are also printed in these configurations similar to as of SRRs extending the range of magnetic response of the composite AMM. Figure 1 shows different configurations of the n^th order rose curve resonator. An edge-coupled inclusion designed by 7th order Rose curve is presented in figure 1 (a). Figure 1 (b) (c) illustrates respectively abroad-side coupled inclusion designed by 7th order Rose curve and a spiral inclusion designed by 13th order Rose curve.

In this work, we comprehensively study the magnetic response of an AMM composed of n-RCR based on its multi design parameters. In fact, the characteristics of this new inclusion are studied and analyzed to underscore the importance of this resonator. We study the impact of the geometrical and physical parameters. In fact, the impact of the order n on the permeability function and the resonant frequency is detailed. In addition, the effect of the area and the perimeter on the resonance frequency and the permeability is studied. As the area and the perimeter are independently tuned by the geometrical parameter of the rose, the effect of this parameter on the magnetic response of the n^th RCR is also presented. Further parametric studies were carried out on the effect of the physical parameters on the magnetic response of the rose curve resonator.

In the following sections, first the magnetic response of the inclusion is modeled and explained. In fact, this model is general and can be used for any shape of the inclusion. Then in Section 3, the nth rose curve resonator is presented. Next in Section 4, using numerical full wave analysis, the magnetic response of the nth rose curve resonator is revealed. Moreover, the simulations are performed for two categories of the rose curve resonator (broad-side coupled inclusion and edge-coupled inclusion). Finally in Section 5, a parametric study is presented to characterize the magnetic spectral response of metamaterials with unit cells of 7^th order rose curve configuration.

2. Modelling Magnetic Response

In fact, it has been proved by Kabiri et al that the physical response of inclusions in AMMs in the presence of electromagnetic field is the same for different inclusions' geometries (2011). Figure 2 illustrates a sample of a unit cell of generic rose curve resonator. By periodically repeating this contour C in a unit cell along a slab, a metamaterial block can be created. In figure 2, the unit cell is defined by a width Δx, depth Δz and height Δy. Therefore, the area and the volume of this unit cell are A= ΔxΔz and V= ΔxΔzΔy=AΔy. In addition, the area of the contour C is denoted by s and its perimeter is denoted by l. The printed inclusion is made with a conductor material defined by an electric conductivity of σ, height of t and width of b. In fact, the resonator is made with two parallel conductor separated with a uniform gap g. The permeability function and the frequency response of the inclusion can be characterized using physical and geometrical properties. As previously shown by kabiri et al. (2009), the resultant permeability of the rose curve resonator can be formulated using physical and geometrical parameters based on a circuit model as:

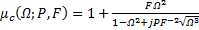
Where is the normalized frequency and is the resonance frequency. F is the fractional area of the cell occupied by the interior of the inclusion and P is a parameter that represents the physical characteristics of the inclusions based on following equations:

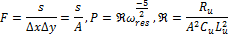
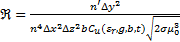
L_u is defined as an inductance per unit area of the inclusion, and R_u, C_u are the per-unit-length resistance and capacitance of the inclusion.

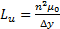
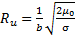
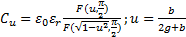
Where 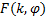is the elliptical Integral of the first kind:

From equation (2), we can notice that the permeability is simply related to the cell dimension, the perimeter and area of the contour, hence, contours with different structure.

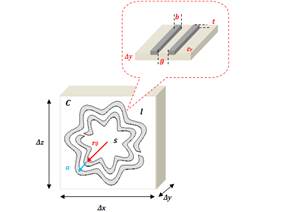
3. N^th Rose Curve Resonator

In this section, the characteristics of the nth order RCRs are discussed. The inductive and capacitive response of RCRs is disjointed by defining the geometry based on multiple parameters.

These curves have a principal characteristic that the area and the perimeter of these rose curves can be adjusted independently. The parameterization of rose curve can be described in polar coordinates by the equation (6):

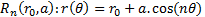
Where r(θ) represents the position of an inclusion's contour in the polar coordinate, and θ is the polar angle which sweeps the contour aside the slit. The parameters r₀ and a are constants and n is an integer representing the order of the curve. Note that, due to its formulation, the area and the perimeter of the rose curve can independently and controllably to be selected in order to achieve enhanced or selected properties of the resonator.

In their work, Kabiri et al. (2011) has shown that the magnetic properties of the metamaterials can be expressed as a function of the geometrical and the physical properties of the inclusions. The perimeter and the area can be considered as the principal geometrical properties of the inclusion. In the structure of the nth order RCR, the area and the perimeter can be calculated using the following expressions:

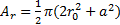
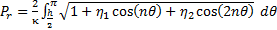
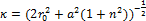
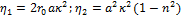
For a specific value of area and perimeter, we can determine the geometrical parameters r₀ and a using the relations (7) and (8). By defining r₀ and a, any structure of the rose curve resonator can be modelled and simulated using numerical full wave analysis. Combining equation (9) and (10) and solving relations (7) and (8)for the specific area and perimeter of the inclusions obtained from a design procedure, the parameters a and r₀ are calculated for any order of the Rose curve. The order of Rose curve determines the number of peaks and troughs on the circle leading to a higher value of the curvature on the inclusion's contour.

4. Simulation of the Magnetic Response

To study the characteristics of RCRs, we have simulated the rose curve resonator in the various topology of broadside-coupled and edge-coupled structure. Figure 3 illustrates magnetic response of the broadside-coupled rose curve resonator (BC-RCR) and the edged-coupled rose curve resonator (EC-RCR). These two resonators are simulated using the same geometrical and physical parameters. Table 1 summarizes the physical parameters of the traces and dimensions of inclusions and it was used to perform the simulation setup.

In the simulation, a substrate with relative dielectric constant ε_r of 2.2 is used (Rogers RT/duroid 5880 (tm)).The thickness of the metal used on the simulation is noted t and it is equal to t= 35 µm and the traces are made with a copper characterized by an electrical conductivity equal to 59.6 s/µm. In fact, in order to simulate the effect of the geometrical parameters on the permeability function, the trace width and the trace gap are respectively fixed to 200 µm and 700 µm.

Table 1. Parameters of the simulated nth order rose curve.

Metal thickness: t= 35 µm

Host medium: Duroid 5880 (εr = 2.2)

Traces: copper (σ = 59.6 s/µm)

Trace width: b= 200 µm

Trace gap: g = 700 µm

Slit width: d=1 mm

The effective permeability of the rose curve resonator is determined from the physical quantities of the reflection coefficient S₁₁ and the transmission coefficient S₂₁. The S-parameters of the unit cell of this rose curve resonator and the position of the resulting resonant frequency have been determined using a time varying electromagnetic field.

In fact, the S-parameters have been simulated with Ansoft HFSS. This full-wave three-dimensional electromagnetic commercial software is used to perform the numerical analysis of the effective parameters.

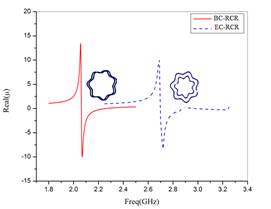
Then, using a developed Matlab application, the Ansoft HFSS results have been converted to desired parameters based on the extraction formula demonstrated by Smith et al (2002) and calculated by Xudong et al (2004). Figure 3 shows the variation of permeability function of the two structures of an RCR with the frequency. For the same geometrical and physical parameters, the edged-coupled rose curve resonator (EC-RCR) resonates at 2.7 GHz but the broadside-coupled rose curve resonator (BC-RCR) resonates at 2.1 GHz. In fact, we can notice that the resonance frequency of the BC-RCR is lower than the resonance frequency of the EC-RCR.

A comparative analysis of both EC-RCR and BC-RCR has been carried out. It has been found that this second resonator shows a lower resonant frequency for the same physical dimensions and permits to have an electrically smaller unit cells. The last property is useful for designing discrete metamaterials with electrically small unit cells. In the following sections, the edged-coupled rose curve resonator (EC-RCR) will be simulated and analysed. So, the simulation will be limited to this structure.

5. Parametric Study of The n^th RCR

In this part, the effect of the dimension cell, the area, the perimeter and the order of RCRs on the magnetic response of the composite AMM are studied. Furthermore, the impact of the physical characteristic on the permeability function is analysed. This parametric study allows characterizing the n-RCR and can be used as a rule guide for design of inclusions with desired magnetic properties.

5. 1. Geometrical Properties of the nth RCR

5. 1.1.The Effect of the Unit Cell Dimension

To study the effect of the dimension cell on the resonant frequency and the permeability function the height Δy of the unit cell is varied from 0.3mm to 0.8mm.The permeability function of the simulated RCR is presented in figure 4.

In fact, the resonant frequency decreases from 0.6 GHz to 0.36 GHz while the height Δy of unit cell increases from 0.3mm to 0.8mm.Though, the maximum amplitude of the permeability function increases from 65 to 140 when the dimension Δy of the unit cell varies from 0.3mm to 0.8mm.

In fact, the inductance per unit area L_u defined by equation (3) is a function of the dimension cell Δy and also the permeability function is expressed using unit cell dimension in equation (2). So, the magnetic response of the nth rose curve resonator is very sensitive to the substrate height.

5. 1.2.The Effect of the Area

To study the effect of the area on the resonant frequency and the permeability function while the perimeter of the inclusion is fixed and the area is varied from 120mm² to 200mm².

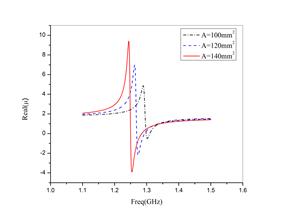
The magnetic response of the simulated RCR is presented in figure 6. In fact, the real part of permeability function is negative near the resonance frequency. Figure 7 illustrates the variation of the resonance frequency versus the area. The resonant frequency decreases from 1.25 GHz to 1.05 GHz while the area increases from 120mm² to 200mm².

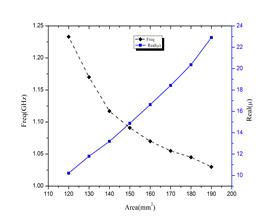
However, the maximum amplitude of the permeability function increases from 10 to 23 when the area varies from 30% to 50% of the unit cell area. The area occupied by the interior of the inclusions tunes the inductance of the inclusions. Hence, when the area occupied by the inclusion increases the resonant frequency decreases. In fact, by knowing the area occupied by the rose curve resonator, the designer can determine the dimensions of the geometrical properties of the inclusion r₀ and a. So, for any predefined geometrical properties of the inclusion, the designer can have an idea about the resonance frequency and the magnetic response of the rose curve resonator.

5. 1. 3. The Effect of the Perimeter

In this section, the 7^th rose curve resonator is simulated for different values of perimeter when the area is fixed to 150mm².

Figure 8 illustrates the frequency response of the permeability functions for different value of the perimeter varied from P=65mm to P=70mm. We observe that the resonant frequency and the maximum amplitude of the permeability function decreases when the perimeter increases. The resonance frequency varies from 0.94 GHz to 0.84 GHz when the perimeter increases.

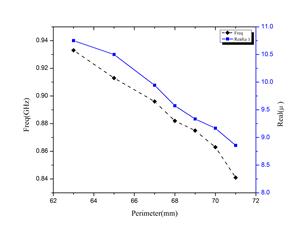
Furthermore, the maximum amplitude of permeability function decreases from 11 to 9. In fact, the effect of the perimeter on the resonant frequency and the maximum amplitude of the permeability function are presented in the figure 9. The capacitive response of an inclusion is tuned by its perimeter geometry. Therefore, the resonant frequency and the permeability decrease while the trace length increases. It can be noticed that inclusion with larger perimeter resonates at lower frequencies.

5. 1.4.The Effect of the Order n

The responses of the inclusions of different orders with identical r₀ and a are very similar in shape. Figure 10 demonstrates the resonant frequency and maximum amplitude of the permeability function versus the order of inclusions.

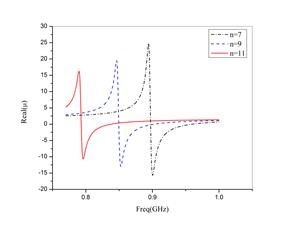
However, the maximum amplitude of the permeability function decreases from 24 to 14 while the order n increases. Moreover, the resonant frequency decreases while the order of the rose curve increases.

The resonance frequency varies from 0.9 GHz to 0.74 GHz when the order increases from 7 to 13. In fact, higher order rose curve resonators introduce the higher coupling factor. In figure 11, we present the variation of the resonance frequency and the maximum amplitude of the permeability.

In fact, increase in order of inclusions decreases the resonant frequency of the inclusions leading to a higher miniaturization of the AMM structure. This enhancement is due to the increase in perimeter length and new capacitive and inductive coupling between the adjacent segments of the rose curve resonator.

5. 2. Physical Properties of the nth RCR

5. 2. 1. The Effect of the Trace Width

Physical properties are variables that are controlled by the designer and the fabrication techniques. The width and height of the printed conductor can be defined as the principle physical parameters that affect the magnetic response of the resonator.

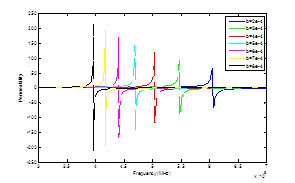
We can also mention the space between parallel printed lines, and material characteristics such as conductivity of the conductor. To study the effect of the physical properties of the inclusion, we simulate the magnetic response of the rose curve resonator. Figure 12 shows the variation of the permeability function versus the frequency from 0.4GHz to 0.6. In fact, the resonance frequency decreases from 0.6 GHz to 0.4 GHz when the values of trace width b increase from 0.2mm to 0.8mm.

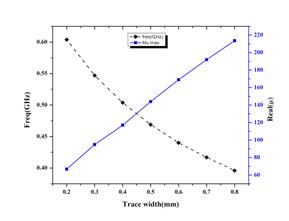
Nevertheless, the amplitude of the permeability function increases from a value of 60 to 200 as the trace width varies from 0.2mm to 0.8mm. We have proved previously that the permeability function was highly sensitive to the physical parameters of the inclusions. Since, the total capacitance and the total resistance of the inclusion are a function of the trace width, the permeability function rapidly varies with the variation of the trace width. Figure 13 illustrates the evolution of the resonance frequency and the maximum amplitude of the permeability with the variation of trace width of the inclusion.

5. 2. 2. The Effect of the Trace Gap

In this part, the effect of the trace gap between the two parallel metal contours of the inclusion is studied. In fact, we analyze the magnetic response of the rose curve resonator between 0.2GHz and 0.8GHz.

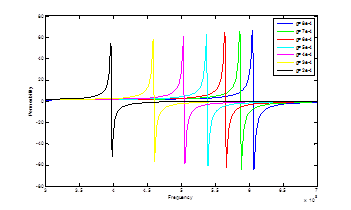
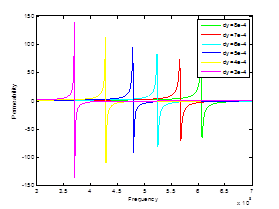
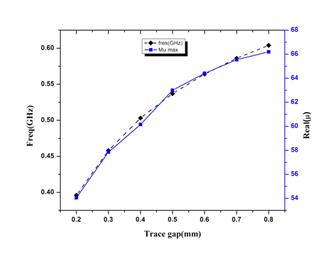
Figure 14 shows the variation of the permeability function versus the frequency for different value of the trace gap noted g. Moreover, both the resonance frequency and the permeability function increase when the values of trace gap g increase. We have earlier noticed that the magnetic response of the inclusion can be considered as a function of the physical parameters of the inclusions. In fact, the total capacitance of the inclusion is a function of the trace gap. Consequently, the resonance frequency varies from 0.4GHz to 0.6GHz with the variation of the trace gap. Similarly, with the variation of the trace gap, the amplitude of the permeability varies from 54 to 66. Figure 15 shows the evolution of the resonance frequency and the maximum amplitude of the permeability with the variation of trace gap of the inclusion.

6. Conclusion

The magnetic behavior of the nth order rose curve resonator (n-RCR) has comprehensively investigated. Using numerical and analytical simulation, this resonator was modeled and studied. A parametric study was performed based on the geometrical and physical characteristics of n-RCR. The area and perimeter and the order of the RCRs are considered as the main parameter of the geometric study. Furthermore, the physical parameters of the trace are used to characterize the spectral magnetic behaviour of the inclusion. It has been observed that the resonant frequency and the permeability function are very sensitive to the area, the circumference and the order of the rose curve resonator. Also, the impact of the physical properties on the permeability function is underscored. In fact, the study can facilitate the design process of rose curve resonators. Moreover, the method performed in parametric study can be utilized in design n-RCRs used as inclusions of an artificial magnetic material with predefined magnetic response.

References